
9-30 to 9-31 A steel bar of thickness h is subjected to a bending force F. The vertical support is stepped such that the horizontal welds are b1 and b2 long. Determine F if the maximum allowable shear stress is τallow.
| Problem Number | b1 | b2 | c | d | h | τallow |
| 9–30 | 2 in | 4 in | 6 in | 4 in |
|
25 kpsi |
| 9–31 | 30 mm | 50 mm | 150 mm | 50 mm | 5 mm | 140 MPa |
Problems 9–30 to 9–31
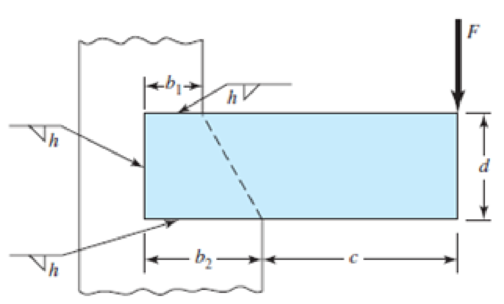
The bending force
Answer to Problem 31P
The bending force
Explanation of Solution
The below figure shows the dimension of the weld.
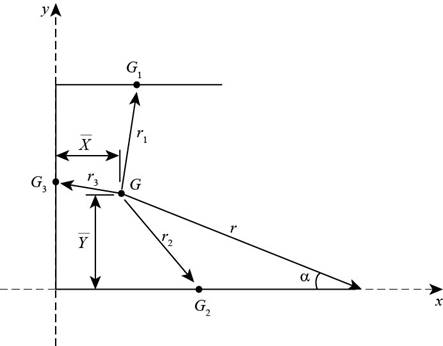
Figure-(1)
Write the expression for throat area of weld-1.
Here, the thickness of weld is
Write the expression for throat area of weld-2.
Here, the length of weld is
Write the expression for throat area of weld-3.
Here, the length of weld is
Write the expression for total throat area.
Write the expression for total length of the weld.
Write the expression for location of centroid along x-direction.
Here, the centroidal length of weld-1 is
Write the expression for centroid along y-direction.
Here, the centroidal distance of weld-1 is
Write the expression for the length between total weld and weld-1.
Write the expression for length between total weld and weld-2.
Write the expression for length of total weld and weld-3.
Write the expression for polar moment of inertia of weld-1 about its centroid.
Write the expression for moment of inertia of weld-2 about its centroid.
Write the expression for polar moment of inertia of weld-3 about its centroid.
Write the expression for polar moment of inertia of the total weld.
Write the expression for length where maximum secondary shear stress occurs.
Write the expression for angle of
Write the expression for moment about weld center.
Here, the load on the weld is
Write the expression for primary shear stress.
Write the expression for secondary shear.
Write the expression for maximum shear stresss.
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Thus, the bending force is
Want to see more full solutions like this?
Chapter 9 Solutions
Shigley's Mechanical Engineering Design (McGraw-Hill Series in Mechanical Engineering)
- An AISI 1050 HR solid tube of 20mm diameter is acted by force F1 = IkN, and force F2 of 2kN. The tube is welded to a larger round base by 3mm fillet weldment, the base is connected to the ground base (shown in gray color) by means of four bolts M8x1.25mm (property class of 4.8)). The bolts are evenly distributed at 20mm away from the center of the tube. R=100 F1 120 120. F2 R=100 D =20 120 R=3 D =60 40 Dimensions are in mm Perform the following the following: 1- Find the state of stress for the most critical point on the assembly and build the mohr's circle. Solve question 1arrow_forwardQ1: The weldment shown in the figure is subjected to a force F. The hot-rolled steel bar has a thickness h and is of AISI 1040 steel. The vertical support is likewise AISI 1040 HR steel. The electrode is given in the table below. Estimate the static load F the bar can carry if two fillet welds are used. b (mm) h (mm) d (mm) 70 Elecrode E8010 30 6 b→→ Farrow_forwardThe steel shafts are connected together using a fillet weld as shown in the figure below. (Figure 1) 12 mm T=60 N-m 12 mm 50 mm- 12 mm 1 12 mm Determine the average shear stress in the weld along section a-s if the torque applied to the shafts is T = 63 N-m. Note: The critical section where the weld fails is along section a-a.arrow_forward
- Q1: The weldment shown in the figure is subjected to a force F. The hot-rolled steel bar has a thickness h and is of AISI 1040 steel. The vertical support is likewise AISI 1040 HR steel. The electrode is given in the table below. Estimate the static load F the bar can carry if two fillet welds are used. b (mm) h (mm) d (mm) 70 Elecrode E8010 30 4arrow_forward1. The welded joint shown below is subjected to a 40 kN of static axial and a 40 kN of static bending loads (F and F1) as shown below. The materials are made of steel with Sut-2070 MPa and Sy=1830MPA. Calculate the factor of safety of the weld. Where, h-6 mm, b-30 mm, c=100 mm d-60 mm, and both forces are equal and each 40 kN (F=F1=40 kN). F F1 d State the reason of your selection in your answer but use only 2 sentences (maximum of 2 lines!) for each answer. 2) Suggest the most suitable bearing type with quantity if a shaft rotates at a speed of 1500 rev/min, subjected to mid-range radial load in a limited radial space. 3) Suggest the most suitable bearing type with quantity if maximum stiffness, stability and resistance to shaft misalignment are desired at a shaft, rotating at 1000 rev/min, under a light radial load. In addition, the shaft is subjected to comparably light thrust loads from either directions. 4) Suggest the most suitable spring type for the following application…arrow_forwardQ1: The weldment shown in the figure is subjected to a force F. The hot-rolled steel bar has a thickness and is of AISI 1040 steel. The vertical support is likewise AISI 1040 HR steel. The electrode is given in the table below. Estimate the static load F the bar can carry if two fillet welds are used. h (mm) b (mm) 30 d (mm) 70 Elecrode E8010arrow_forward
- The figure below shows two plates connected by two rivets. The plates are made from aluminum 6061-T6 and the rivets are made from aluminum 2014-T4. Evaluate the maximum allowable force on the connection to meet the following design criteria: (a) The shear stress in a rivet cannot exceed 14 of the ultimate strength in shear. (b) The tensile stress in the plates cannot exceed 13 of the yield strength. (c) The bearing stress on either the plates or the rivets cannot exceed the design bearing stress 9 mm 75 mm 38 mm 38 mm 12 mm dia. 9 mmarrow_forwardA beam 1m long with dimensions b = 50 mm and d = 100 mm is subjected to a load of 500 kgs as shown. A 7018 electrode is used to weld the beam section all around. Weld size is 12 mm. Approximate the maximum stress in the weld. Compare the maximum weld stress with the strength of the electrode. F 12 -Xarrow_forwardQ1: The weldment shown in the figure is subjected to a force F. The hot-rolled steel bar has a thickness h and is of AISI 1040 steel. The vertical support is likewise AISI 1040 HR steel. The electrode is given in the table below. Estimate the static load F the bar can carry if two fillet welds are used. d (mm) h (mm) Elecrode b (mm) 30 70 6 E8010 4 ko →arrow_forward
- Ql: The steel strap with thickness of 12 mm is to be welded to a rigid frame to carry a static load of F=20 kN. The strap and frame are welded together by fillet welds along two sides. Using the maximum distortion energy theory, determine the minimum length of the weld to be on safe side. The yield strength is 420 MPa. The safety factor should be considered as 4. (k=12 mm)arrow_forwardTwo bars are connected with a welded butt joint as shown. The bar dimensions are b = 200 mm and t = 50 mm, and the angle of the weld is a = 45°. The bars transmit a force of P = 301 kN. What is the magnitude of the average shear stress that acts on plane AB? Weld В P A Answer: T= i MPаarrow_forwardSituation 2: The lap splice shown will develop a full strength as shown in the figure. Using E70 electrodes. The width of the plate is 150 mm and the thickness is 10 mm. Use Fy = 248 MPa T4 46 mm 48 mm 1. Which of the following nearly gives the diameter of the slot weld using the LRFD method. O 45 mm T O 47 mm T Warrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





