
(a)
The elements of M matrix in terms of elements of S matrix,
(a)
Answer to Problem 2.54P
The elements of M matrix in terms of elements of S matrix is
Explanation of Solution
The element B can be expressed as follows,
The element F can be expressed as follows,
Use the value of G from the equation (I) in (II).
From the equation (I) and (III), the matric M can be written as follows.
Similarly define the element G and solve for
Similarly define the element F and solve for
Use the value of B from the equation (V) in (VI).
From equation (V), and (VII).
From the equation (V),
From the equation (VII),
From the equation (V),
From the equation (VII),
Conclusion:
Therefore, the elements of M matrix in terms of elements of S matrix is
(b)
Show that M matrix for the combination is the product of the two M matrix for each section separately.
(b)
Answer to Problem 2.54P
Showed that M matrix for the combination is the product of the two M matrix for each section separately.
Explanation of Solution
Consider the Figure below.
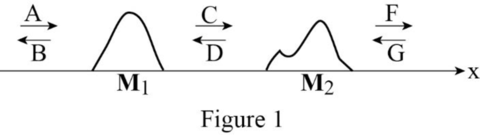
Consider the matrix.
Consider the matrix.
Use equation (XIV) in (XIII).
Hence proved.
Conclusion:
Therefore, the M matrix for the combination is the product of the two M matrix for each section separately.
(c)
The matrix for the scattering from a single delta function potential at point a.
(c)
Answer to Problem 2.54P
The matrix for the scattering from a single delta function potential at point a is
Explanation of Solution
The wave function for the scattering from a single delta function potential at point a is
Using the continuity condition of the wave function, equation (XV) can be written as.
Using the discontinuity condition of the derivative of wave function, equation (XV) can be written as.
Multiply the equation (XVI) with
Multiply the equation (XVII) with
Add equation (XVIII) and (XIX), and solve for
Where,
Subtract equation (XIX) from (XVIII), and solve for
From equation (XX), and (XXI), the matrix can be written as follows.
Conclusion:
Therefore, the matrix for the scattering from a single delta function potential at point a is
(d)
The matrix for scattering from the double delta function, and the transmission coefficient for this potential.
(d)
Answer to Problem 2.54P
The matrix for scattering from the double delta function is
Explanation of Solution
The matrix
From the result of part (b), the matrix for scattering from the double delta function can be expressed as.
The transmission coefficient can be calculated using the equation (XXIV).
Simplify the equation (XXV).
Conclusion:
Therefore, The matrix for scattering from the double delta function is
Want to see more full solutions like this?
Chapter 2 Solutions
Introduction To Quantum Mechanics
- Consider the Initial Value Problem: X₁ 01 x²₁ x₂ = (a) Find the eigenvalues and eigenvectors for the coefficient matrix. 181 An ellipse with clockwise orientation the trajectory. = - 3x1 + 3x₂ -6x₁ + 3x₂² (b) Solve the initial value problem. Give your solution in real form. I1 = 1-8 x2 = *1(0) x2(0) and X2 = = = ໜຶ່ງ : = 27 18 1. Use the phase plotter pplane9.m in MATLAB to describearrow_forwardDivergence theorem. (a) Use the divergence theorem to prove, v = -478 (7) (2.1) (b) [Problem 1.64, Griffiths] In case you're not persuaded with (a), try replacing r by (r² + e²)2 and watch what happens when ɛ → 0. Specifically, let 1 -V². 4л 1 D(r, ɛ) (2.2) p2 + g2 By taking note of the defining conditions of 8°(7) [(1) at r = 0, its value goes to infinity, (2) for all r + 0, its value is 0, and (3) the integral over all space is 1], demonstrate that 2.2 goes to 8*(F) as ɛ → 0.arrow_forwardProblem 1.15 Calculate the divergence of the following vector functions: (a) va = x² + 3xz²ŷ - 2xz2.arrow_forward
- Prove that for any vector u, u = (u e,)e, +(u ·e, )e, + (u e,)e,. [Hint: write u in component form.] Find the projection of the vector u e, -2e, +e, on the vector 2. 3. v = 4e, - 4e, + 7e,.arrow_forward2.7 There are certain simple one-dimensional problems where the equation of motion (Newton's second law) can always be solved, or at least reduced to the problem of doing an integral. One of these (which we have met a couple of times in this chapter) is the motion of a one-dimensional particle subject to a force that depends only on the velocity v, that is, F = F(v). Write down Newton's second law and separate the variables by rewriting it as m dv/F(v) = dt. Now integrate both sides of this equation and show that t = m v dv' F(v¹) Vo Provided you can do the integral, this gives t as a function of v. You can then solve to give v as a function of t. Use this method to solve the special case that F(v) = Fo, a constant, and comment on your result. This method of separation of variables is used again in Problems 2.8 and 2.9.arrow_forward(a) Find the scalar products î · î, ĵ· ĵ, and k · Ê. (b) Find î · ĵ, ĵ · k, and k · î (c) Use the distributive law to multiply out the scalar product of two arbitrary vectors à Axî + Ayî + A¸k and B Equation 6.4. Bxî + Byĵ + Bzk, and use the results of (a) and (b) to verifyarrow_forward
- How is it that I can have b=x in problem 7.48?arrow_forwardThe figure shows two railway cars with a buffer spring. We want to investigate the transfer of momentum that occurs after car 1 with initial velocity v0 impacts car 2 at rest. The differential equation is given below. Show that the eigenvalues of the coefficient matrix A are λ1=0 and λ2=−c1−c2, with associated eigenvectors v1= 1 1 T and v2= c1 −c2 T. x′′= −c1 c1 c2 −c2 x with ci=k /mi for i=1, 2 The coefficient matrix A is .arrow_forwardHow would I be able to sketch the graph in problem 7.36?arrow_forward
- Find the derivative of each function at the given point and interpret the physical meaning of this quantity. Include units in your answer The gravitational force of attraction between two masses separated by a distance of x meters is inversely proportional to thesquare of the distance between them, which implies that the forceis described by the function F(x) = k/x2, for some constant k,where F(x) is measured in newtons. Find F′(10), expressing youranswer in terms of karrow_forwardOur unforced spring mass model is mx00 + βx0 + kx = 0 with m, β, k >0. We know physically that our spring will eventually come to rest nomatter the initial conditions or the values of m, β, or k. If our modelis a good model, all solutions x(t) should approach 0 as t → ∞. Foreach of the three cases below, explain how we know that both rootsr1,2 =−β ± Sqrt(β^2 − 4km)/2mwill lead to solutions that exhibit exponentialdecay.(a) β^2 − 4km > 0. (b) β^2 − 4km =0. (c) β^2 − 4km >= 0.arrow_forwardConsider a rectangular surface of length L and width W in the xy plane with its center at the origin: Which of the following are valid expressions for the area vector of this surface? Check all that apply. O (0,0, LW) O (W, L, 0) O (0,0, -LW) O (LW, LW, 0) O (0, LW, 0) O (L, W, 0)arrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





